Professor Haiyan Gao of Duke University and Professor Dipangkar Dutta of Mississippi State University outline the multifaceted nature of the proton through its size.
The proton is the lightest (hydrogen) nucleus. It is Greek for ‘first’, as named by Rutherford in 1920, when he discovered it as the elementary constituent extracted from the nitrogen nucleus through atomic collisions.¹ The proton (as well as the neutron) is known as a nucleon, a building block of atomic nuclei responsible for more than 99% of visible matter in the Universe. The proton was considered a fundamental particle (without internal structure) until the discovery of its internal partonic structure from the deep inelastic scattering experiment led by Friedman, Kendall, and Taylor in the 1960s.²
We now know that the structure of the proton is dynamic and rich, consisting of quarks and gluons, which are the fundamental degrees of freedom of quantum chromodynamics (QCD), the theory of the strong force. QCD is an important part of the Standard Model (SM) of particle physics, which successfully unifies electromagnetic, weak, and strong forces. Within the SM, our knowledge of confinement and how QCD works remains limited due to our inability to solve QCD analytically.
Major progress has been made on simulating QCD on computers, known as lattice QCD, to predict the properties and structure of the nucleon. Protons provide a laboratory not only for advancing our knowledge of QCD, but also for searches for new physics beyond the Standard Model, as the SM can’t explain observations such as dark matter, dark energy, and the baryon number asymmetry of the Universe.
Proton radii
The proton is often pictured as a smooth sphere; however, with it being a quantum mechanical object, determining its size is nontrivial. Several different facets of the proton’s structure can be used to define its radius. Among quantities related to the structure of the proton, the proton charge radius, defined as the root-mean-squared charge radius (rp), describes the size of the proton weighted by its internal charge distribution. It is by far the most popular and best-known proxy for the size of the proton, first measured by Hofstadter in the 1950s by scattering electrons elastically from protons in a hydrogen target.³ The proton charge radius is particularly interesting and important for both advancing QCD and high-precision tests of quantum electrodynamics (QED). Such advancement requires significantly more precise determination than that from the original Hofstadter experiment.
Other radii are associated with the proton, such as its magnetic radius, mass, pressure, and polarizability radius. The magnetic radius of the proton, like the charge radius, is the size of the proton weighted by its magnetisation distribution. The mass of the proton is particularly interesting because it is mostly due to interactions, i.e., due to the gluons and not from the mass of the quarks inside. Therefore, naïvely the proton mass radius is roughly the radius of the gluon distribution inside the proton. Unlike the proton charge radius, the experimental determination of its mass radius is at an early stage, and one promising approach is through near-the-threshold production of the J/ψ meson from the proton. Such production is expected to be dominated by multi-gluon exchange, therefore, sensitive to the mass radius. Early indications are that this radius is smaller than the proton charge radius.⁴
The pressure or mechanical radius of the proton, which is related to its gravitational properties, is also fundamental and interesting. With the gravitational constant being many orders of magnitude smaller than the coupling constant of even the weak force, it is inconceivable to even imagine scattering gravitons from the proton. A clever way to possibly access the pressure distribution of quarks inside the proton is through the deeply virtual Compton scattering (DVCS) process. In DVCS, the virtual photon from an electron scattering off a proton couples to a quark inside and produces a real photon in the final state. The virtual photon and the real photon together mimic the spin-2 graviton, allowing access to the radial pressure distribution in the proton. Like the proton mass radius, such studies are at a very early stage and model-dependent.⁵ Meanwhile, lattice QCD has been making promising strides in predicting these radii, including the proton charge radius.⁶
Experimental methods of measuring the proton charge radius
There are two experimental methods to determine rp, and they are lepton (electron or muon) scattering, pioneered by Hofstadter, and atomic spectroscopy involving measuring atomic transitions. With the former, lepton (electron, muon) beams can be used, though the most commonly used is electron scattering. Electron-proton elastic scattering is an electromagnetic process and is dominated by a one-photon exchange in which a virtual photon carrying a 4-momentum of Q is exchanged between an electron and a proton. For a spin-1/2 object such as a proton, the elastic cross section is determined for each value of momentum transfer squared (Q²) by the electric and magnetic form factors, which are related to the charge and magnetic moment distributions inside the proton.
These form factors are typically measured by analysing the momentum and angle of the scattered electron using a magnetic spectrometer. The proton charge radius can be extracted from the slope of the proton electric form factor at Q²=0. Experimentally, however, one can never reach the Q²=0 value; therefore, an extrapolation to the zero point is required from data to extract the rp.
For the spectroscopy method (see Fig. 1), ordinary hydrogen atoms have been used for decades before such a spectroscopic approach was successfully innovated in an experiment using muonic hydrogen at the Paul Scherrer Institute (PSI) by the CREMA (Charge Radius Experiments with Muonic Atoms) collaboration. A muonic hydrogen atom is like an ordinary hydrogen atom, but the electron orbiting the proton is replaced by a muon, with a mass about 200 times that of an electron. The Bohr radius of a muonic hydrogen atom is therefore significantly smaller than that of an ordinary hydrogen atom. As such, muonic hydrogen spectroscopic measurements are more sensitive to the proton charge radius. There are two types of spectroscopic measurements. The first is Lamb shift or an equivalent with transition involving energy levels of the same principal quantum number, and measuring one transition is sufficient. The other involves transition between levels of different principal quantum numbers, and two different transitions are needed to determine both the proton radius and the Rydberg constant.
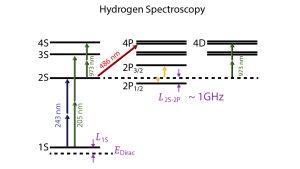
The first PSI result released in 2010 provided the most precise measurement of this quantity.⁷ However, it is several standard deviations smaller than the Committee on Data recommendation, known as the CODATA value, compiled from electron scattering and ordinary hydrogen spectroscopic measurements. On the other hand, the result from a concurrent and extensive electron scattering campaign at Mainz University was consistent with the CODATA value.⁸ The PSI 2013⁹ result confirmed its original 2010 result with even better precision. These two results triggered the famous proton charge radius puzzle and motivated worldwide efforts in both experiment and theory to resolve the puzzle.
Is this puzzle due to accidental omission of important physics in theoretical calculations, experimental issues, or beyond-the-standard-model (BSM) physics, such as the breaking of lepton universality?
The PRad and PRad-II experiment
Shortly thereafter, the first magnetic-spectrometer-free electron scattering experiment on regular hydrogen atoms, known as the PRad experiment, was performed to address the proton radius puzzle. The experiment used the world’s most intense electron beam from the Continuous Electron Beam Accelerator Facility (CEBAF) at Jefferson Lab. The PRad experiment innovated on several fronts to make it one of the most precise electron scattering measurements.
One innovation involved combining a special high-resolution calorimeter with a gas-electron multiplier (GEM)-based coordinate detector, covering a wide range of electron scattering angles in a single setting and reaching the smallest scattering angle ever. This ensures that the extrapolation to Q²=0 (i.e., zero angle) is robust and the associated uncertainties are well controlled.
The second innovation was utilising an internal target by continuously flowing cryogenically cooled hydrogen atoms through a tube with no end caps and with a set of powerful pumps to remove the hydrogen leaving the tube and maintain the required beamline vacuum. Eliminating scattering from target windows and using the calorimeter allowed access to the most forward scattering angle that previous experiments were unable to reach.
The third innovation was the simultaneous detection of electrons scattered from both the proton and the electron in the hydrogen atom. Doing so eliminates the need to know exactly how many hydrogen atoms were hit by how many total accumulated electrons from the beam. This aspect contributed to one of the largest systematic uncertainties in all previous electron scattering experiments. The radius resulting from the PRad experiment is consistent with the muonic hydrogen results but smaller than those from previous electron scattering experiments.10
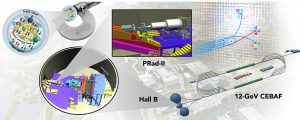
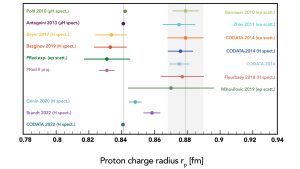
The PRad experiment made a major step toward resolving the proton charge radius puzzle and demonstrated the advantages of the novel magnetic-spectrometer-free technique. However, being the first of its kind, it did not reach the highest precision that this innovative method is capable of. Therefore, an upgraded experiment, known as PRad-II (see Fig. 2), is currently under construction at Jefferson Lab. The PRad-II result is expected to be about three times more precise compared with PRad (see Fig. 3), with better control over the experimental backgrounds thanks to major upgrades that include adding a second plane of GEM and accessing even smaller scattering angles by installing a scintillator veto detector. The new experiment11 has been designed to reduce major systematic uncertainties encountered by the PRad experiment, which is important in resolving discrepancies with previous electron scattering experiments. It will push electron scattering experiments to reach the same level of precision as hydrogen spectroscopy experiments, establishing a new precision frontier to fully resolve the proton radius puzzle and probe BSM physics.
Other charge radius experiments
During these intervening years, five new and improved hydrogen spectroscopy experiments have also been completed. Four of these experiments, including the Lamb shift measurement, have found a smaller proton radius like the muonic hydrogen measurements, and achieved somewhat better precision compared with previous, ordinary hydrogen spectroscopy measurements. As a result, the CODATA12 value of the charge radius has been updated to a smaller value while also shifting the Rydberg constant, one of the most precisely measured constants in physics.
To date, there has not been a result on the proton charge radius from muon scattering. To remedy this situation, a new muon scattering experiment (called MUSE)13 is currently underway at PSI in Switzerland. This experiment has the distinction of simultaneously measuring the charge radius by scattering positively and negatively charged muons as well as electrons and positrons from a hydrogen target. In addition to measuring the charge radius of the proton, this experiment has been designed to directly verify lepton universality.
Yet another unique muon scattering experiment, called AMBER,14 under construction at CERN, will use muons scattering from an active hydrogen target to detect recoiling protons. Several other electron scattering experiments that are improved versions of the traditional magnetic-spectrometer-based measurements are also underway or being planned. One is the ULQ2 experiment15 in Japan, which completed its data-taking. Another such experiment, called MAGIX,16 will use a hydrogen gas jet target to help eliminate the background from target windows.
The proton charge radius puzzle is being addressed by a large variety of intense experimental efforts and is expected to be satisfactorily resolved within the next several years.
Summary
In more than a century since the discovery of the proton, scientists have made dramatic strides in understanding the very complex and multifaceted structure of the proton. Along the way, there have been many surprising twists and turns. The size of the proton and the myriad ways to describe its size are just one aspect of its complex structure, but it has all the hallmarks of a wonderful story and a faithful reflection of the scientific method.
Acknowledgements
We thank Matthew Cahill, Christopher Guthrie, Michael Hall, and Shannon West from Jefferson Lab for their help, along with the PRad Collaboration. The authors acknowledge the support from the Nuclear Physics Office of Science of the U.S. Department of Energy.
References
E. Rutherford, Phil Mag., 37, 581 (1919).
E. D. Bloom et al., Phys. Rev. Lett. 23, 930 (1969).
R. W. McAllister and R. Hofstadter, Phys. Rev. 102, 851 (1956).
B. Duran et al., Nature 615, 813 (2023).
V. D. Burkert, L. Elouadrhiri and F. X. Girod, Nature 557, 396 (2018).
C. Alexandrou et al., Phys. Rev. D 101, 114504 (2020).
R. Pohl et al., Nature 466, 213 (2010).
J. C. Bernauer et al., Phys. Rev. Lett. 105, 242001 (2010).
A. Antognini et al., Science 339, 417 (2013).
W. Xiong et al., Nature (London) 575, 147 (2019).
A. Gasparian et al., arXiv:2009.10510.
E. Tiesinga, P. J. Mohr, D. B. Newell, and B. N. Taylor, CODATA 2018, Rev. Mod. Phys. 93, 025010 (2021); P. J. Mohr, D. B. Newell, B. N. Taylor and E. Tiesinga, CODATA 2022, Rev. Mod. Phys. 97, 025002 (2025).
R. Gilman et al., (MUSE Collaboration), arXiv:1303.2160, arXiv:1709.09753.
C. Dreisbach et al., (COMPASS++/AMBER Working Group), 2019, Proc. Sci. DIS2019, 222.
T. Suda, https://indico.cern.ch/event/1459380/contributions/6525077/attachments/3078184/5447891/PAW25_Suda.pdf
https://magix.uni-mainz.de
Please note, this article will also appear in the 24th edition of our quarterly publication.
Source link

